Ramas de la Matemática: Conceptos importantes de la Geometría

La Geometría se propone ir más allá de lo alcanzado por la intuición. Por ello, es necesario un método riguroso, sin errores; para conseguirlo se han utilizado históricamente los sistemas axiomáticos.

El primer sistema axiomático lo establece Euclides, aunque era incompleto. David Hilbert propuso a principios del siglo XX otro sistema axiomático, este ya completo. Como en todo sistema formal, las definiciones, no solo pretenden describir las propiedades de los objetos, o sus relaciones. Cuando se axiomatiza algo, los objetos se convierten en entes abstractos ideales y sus relaciones se denominan modelos.

Esto significa que las palabras “punto”, “recta” y “plano” deben perder todo significado material. Cualquier conjunto de objetos que verifique las definiciones y los axiomas cumplirá también todos los teoremas de la geometría en cuestión, y sus relaciones serán virtualmente idénticas al del modelo “tradicional”.

Los siguientes son algunos de los conceptos más importantes en geometría

Puntos:

Los puntos se consideran objetos fundamentales en la geometría euclidiana y se han definido de diversas formas, incluida la definición de Euclides como "aquello que no tiene parte" y mediante el uso de álgebra o conjuntos anidados.

En muchas áreas de la geometría, como la geometría analítica, la geometría diferencial y la topología, se considera que todos los objetos se construyen a partir de puntos, sin embargo, se ha realizado algún estudio de geometría sin referencia a puntos.

Líneas:

Euclides describió una línea como "longitud sin ancho" que "se encuentra igualmente con respecto a los puntos sobre sí misma".  En las matemáticas modernas, dada la multitud de geometrías, el concepto de línea está estrechamente relacionado con la forma en que se describe la geometría.

Por ejemplo, en geometría analítica, una línea en el plano a menudo se define como el conjunto de puntos cuyas coordenadas satisfacen una ecuación lineal dada, pero en un entorno más abstracto, como la geometría de incidencia, una línea puede ser un objeto independiente, distinto del conjunto de puntos que se encuentran en él. 

En geometría diferencial, una geodésica es una generalización de la noción de línea a espacios curvos.

Planos:

Un plano es una superficie plana bidimensional que se extiende infinitamente.  

Los planos se utilizan en todas las áreas de la geometría.

Por ejemplo, los planos se pueden estudiar como una superficie topológica sin hacer referencia a distancias o ángulos; se puede estudiar como un espacio afín, donde se pueden estudiar la colinealidad y las proporciones, pero no las distancias se pueden estudiar como el plano complejo utilizando técnicas de análisis complejo y así sucesivamente.

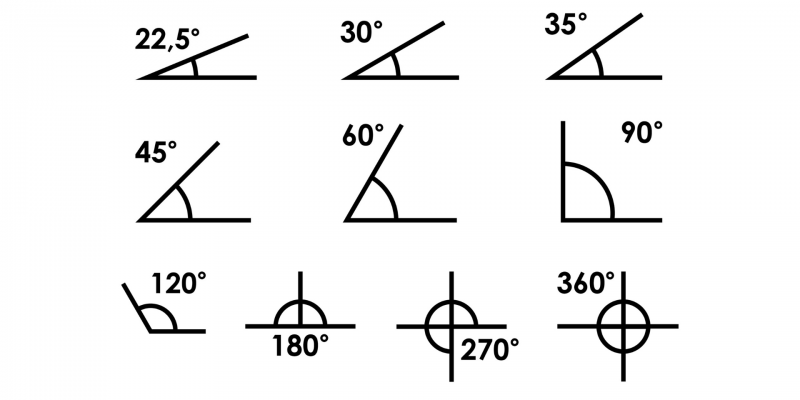
Ángulos:

Euclides define un ángulo plano como la inclinación entre sí, en un plano, de dos líneas que se encuentran y no son rectas entre sí. 

En términos modernos, un ángulo es la figura formada por dos rayos, llamados lados del ángulo, que comparten un punto final común, llamado vértice del ángulo.

Superficies:

Una superficie es un objeto bidimensional, como una esfera o un paraboloide.  

En geometría diferencial y topología, las superficies se describen mediante "parches" bidimensionales (o vecindades) que se ensamblan mediante difeomorfismos u homeomorfismos, respectivamente.

En geometría algebraica, las superficies se describen mediante ecuaciones polinómicas.

Longitud, área y volumen:

La longitud, el área y el volumen describen el tamaño o la extensión de un objeto en una dimensión, dos dimensiones y tres dimensiones, respectivamente. 

En geometría euclidiana y geometría analítica, la longitud de un segmento de línea a menudo se puede calcular mediante el teorema de Pitágoras. 

El área y el volumen pueden definirse como cantidades fundamentales separadas de la longitud, o pueden describirse y calcularse en términos de longitudes en un plano o espacio tridimensional. 

Los matemáticos han encontrado muchas fórmulas explícitas para el área y fórmulas para el volumen de varios objetos geométricos.

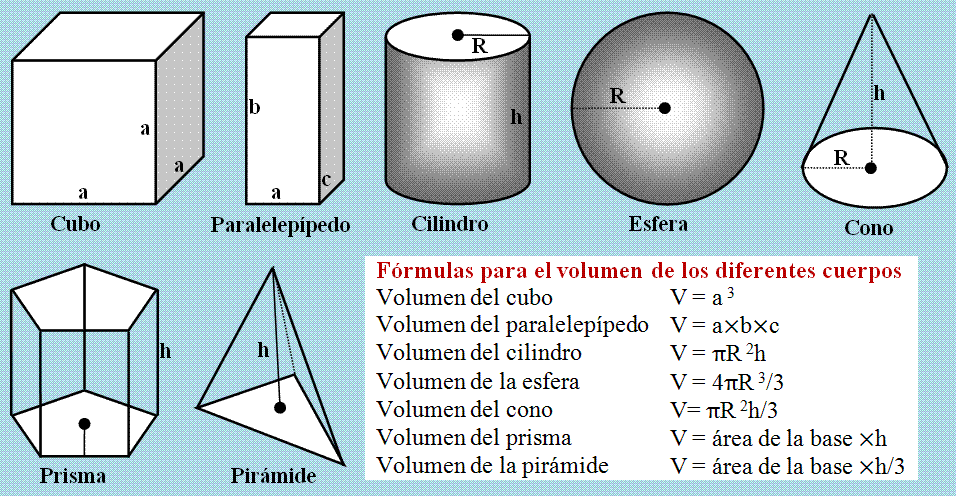
En cálculo, el área y el volumen se pueden definir en términos de integrales, como la integral de Riemann o la integral de Lebesgue.

Congruencia y similitud:

La congruencia y la similitud son conceptos que describen cuando dos formas tienen características similares.  

En la geometría euclidiana, la similitud se usa para describir objetos que tienen la misma forma, mientras que la congruencia se usa para describir objetos que son iguales tanto en tamaño como en forma.  

"Congruencia"

“Similitud"

Hilbert, en su trabajo sobre la creación de una base más rigurosa para la geometría, trató la congruencia como un término indefinido cuyas propiedades están definidas por axiomas.

La congruencia y la similitud se generalizan en la geometría de transformación, que estudia las propiedades de los objetos geométricos que se conservan mediante diferentes tipos de transformaciones.

Por si quieres saber más sobre los Conceptos de la Geometría mira el siguiente video: