La civilización India y las Matemáticas

India y las Matemáticas:

La matemática india o matemática hindú logró una importancia capital en la cultura occidental prerrenacentista con el legado de sus cifras, incluyendo el numeral cero (0), para denotar la ausencia de una unidad en la notación posicional.

Las primeras matemáticas conocidas en la historia de la India datan del 3000 - 2600 a. C., en la Cultura del Valle del Indo (civilización Harappa) del norte de la India y Paquistán.

Esta civilización desarrolló un sistema de medidas y pesas uniforme que usaba el sistema decimal, una sorprendentemente avanzada tecnología con ladrillos para representar razones, calles dispuestas en perfectos ángulos rectos y una serie de formas geométricas y diseños, incluyendo cuboides, barriles, conos, cilindros y diseños de círculos y triángulos concéntricos y secantes.

Los instrumentos matemáticos empleados incluían una exacta regla decimal con subdivisiones pequeñas y precisas, unas estructuras para medir de 8 a 12 secciones completas del horizonte y el cielo y un instrumento para la medida de las posiciones de las estrellas para la navegación.

La escritura hindú probablemente no ha sido descifrada todavía, de ahí que se sepa muy poco sobre las formas escritas de las matemáticas en Harappa. Hay evidencias arqueológicas que han llevado a algunos a sospechar que esta civilización usaba un sistema de numeración de base octal y tenían un valor para π, la razón entre la longitud de la circunferencia y su diámetro.12

No obstante, fue durante el período clásico (siglos I al VIII) cuando los matemáticos indios llegaron a la madurez. Con anterioridad a este período, los hindúes tuvieron algún contacto con el mundo griego. La marcha de Alejandro Magno sobre la India tuvo lugar durante el siglo IV a. C.

Por otra parte, la expansión del budismo en China y la del mundo árabe multiplicaron los puntos de contacto de la India con el exterior. Sin embargo, las matemáticas hindúes se desenvolvieron en un plano original, apoyándose más en el cálculo numérico que en el rigor deductivo.

Los avances en matemática india posteriores a los Sulba Sutras son los Siddhantas, tratados astronómicos del período Gupta (siglos IV y V d. C.) que muestran una fuerte influencia helénica. Son significativos en cuanto a que contienen la primera instancia de relaciones trigonométricas basadas en una semi-cuerda, como en trigonometría moderna, en lugar de una cuerda completa, como en la trigonometría ptolemaica. Con una serie de alteraciones y errores de traducción de por medio, las palabras «seno» y «coseno» derivan del sánscrito jiya y kojiya.

El Suria-sidhanta (hacia el año 400) introdujo las funciones trigonométricas de seno, coseno y arcoseno y estableció reglas para determinar las trayectorias de los astros que son conformes con sus posiciones actuales en el cielo. Los ciclos cosmológicos explicados en el texto, que eran una copia de trabajos anteriores, correspondían a un año sideral medio de 365.2563627 días, lo que solo es 1,4 segundos mayor que el valor aceptado actualmente de 365.25636305 días. Este trabajo fue traducido del árabe al latín durante la Edad Media.

En el siglo V, Aryabhata escribe el Aryabhatiya, un delgado volumen concebido para complementar las reglas de cálculo utilizadas en astronomía y en medida matemática. Escrito en verso, carece de rigor lógico o metodología deductiva.

Aunque casi la mitad de las entradas son incorrectas, es en el Aryabhatiya en donde el sistema decimal posicional aparece por vez primera. Siglos más tarde, el matemático árabe Abu Rayhan Biruni describiría este tratado como «una mezcla de guijarros ordinarios y cristales onerosos».

En 499, Aryabhata introdujo la función verseno, produjo las primeras tablas trigonométricas del seno, desarrolló técnicas y algoritmos de álgebra, infinitesimales, ecuaciones diferenciales y obtuvo la solución completa de ecuaciones lineales por un método equivalente al actual, además de cálculos astronómicos basados en un sistema heliocéntrico de gravitación. Desde el siglo VIII estuvo disponible una traducción al árabe de su Ariabhatiya, seguida de una traducción al latín en el siglo XIII. También calculó el valor de π con once decimales (3,14159265359).

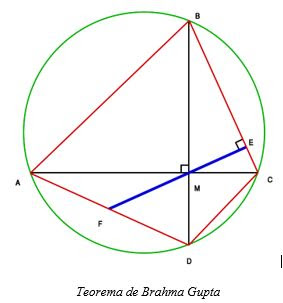
En el siglo VII, Brahma Gupta identificó el teorema de Brahma Gupta, la identidad de Brahma Gupta y la fórmula de Brahma Gupta y, por primera vez en Brahma-sphuta-siddhanta, explicó claramente los dos usos del número 0: como un símbolo para rellenar un hueco en el sistema posicional y como una cifra y explicó el sistema de numeración hindo-arábigo.

Fue a raíz de una traducción de este texto indio sobre matemáticas (hacia el 770) cuando las matemáticas islámicas tuvieron acceso a este sistema de numeración, que posteriormente adaptaron usando los numerales arábigos.

Los estudiantes árabes exportaron este conocimiento a Europa hacia el siglo XII y terminó desplazando los sistemas de numeración anteriores en todo el mundo. En el siglo X, un comentario de Jalaiuda sobre la obra de Pingala incluía un estudio de la sucesión de Fibonacci y del triángulo de Pascal y describía la formación de una matriz.

En el siglo XII, Bhaskara II estudió diversas áreas de las matemáticas. Sus trabajos se aproximan a la moderna concepción de infinitesimal, derivación, coeficiente diferencial y diferenciación.

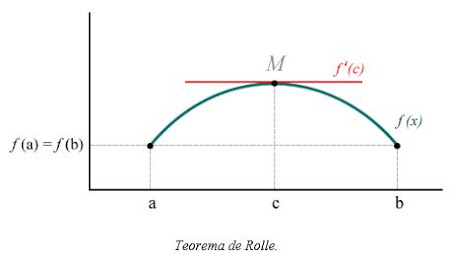
También estableció el teorema de Rolle (un caso especial del teorema del valor medio), estudió la ecuación de Pell e investigó la derivada de la función seno. Hasta qué punto sus aportes anticiparon la invención del cálculo es fuente de controversias entre los historiadores de las matemáticas

Desde el siglo XII, Mádhava, fundador de la Escuela de Kerala, encontró la llamada serie de Madhava-Leibniz y, utilizando 21 términos, computó el valor del número π a 3,14159265359.

Mádhava también encontró la serie de Madhava-Gregory para el arcotangente, la serie de potencias Madhava-Newton para determinar el seno y el coseno, así como las aproximaciones de Taylor para las funciones seno y coseno.

En el siglo XVI, Jyesthadeva consolidó muchos de los desarrollos y teoremas de la Escuela de Kerala en los Yukti-bhāṣā. Sin embargo, la Escuela no formuló una teoría sistemática de la derivada o la integración, ni existe evidencia directa de que sus resultados hayan sido transmitidos al exterior de Kerala.

Por si quieres saber más sobre India y las Matemáticas observa el siguiente video: